MECÂNICA GERAL
Dado o esquema a seguir,
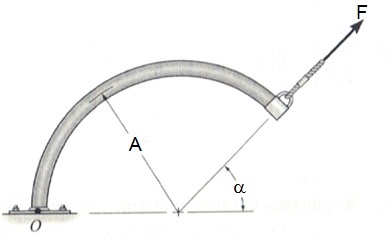
Considerando o ângulo alpha  , igual 42°, F = 0,8 kN, o momento da força em relação ao ponto O igual
, igual 42°, F = 0,8 kN, o momento da força em relação ao ponto O igual  kN.m, então o valor de A será exatamente
kN.m, então o valor de A será exatamente
1,2 m.
1,5 m.
2,5 m.
2 m.
1 m.
Determine o esforço cortante em C e o momento fletor em D da viga. Assuma que B seja um rolete e que C está localizado logo à direita da carga de 40 kN.
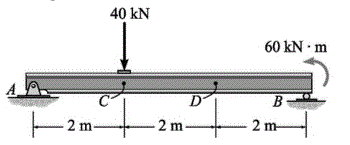
VC = 4,8 kN
MD = - 75,8 kN.m
VC = -3,33 kN
MD = 66,67 kN.m
VC = 2,5 kN
MD = 49,2 kN.m
VC = -2,45 kN
MD = 25,7 kN.m
VC = -6,66 kN
MD = 32,67 kN.m
O cubo da roda pode ser conectado ao eixo com deslocamento negativo (esquerda) ou com deslocamento positivo (direita). Se o pneu está sujeito às cargas normal e radial conforme mostrado,
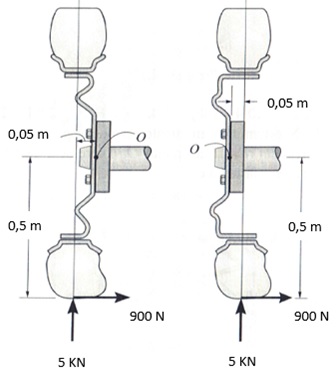
Então o momento resultante dessas cargas em relação ao ponto O no eixo para os dois casos são respectivamente
200 N.m, 700 N.m
200 N.m, 800 N.m
120 N.m, 225 N.m
344 N.m, 225 N.m
350 N.m, 600 N.m
É correto afirmar em relação as intensidades das forças F1, F2 e F3, de modo que a partícula seja mantida em equilíbrio, que:
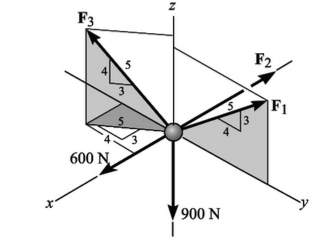
F2=F1
F1
F2
F1
F2
Calcule as reações de apoio,RAy , RBy e RBx do esquema abaixo (móvel em A, fixo em B):
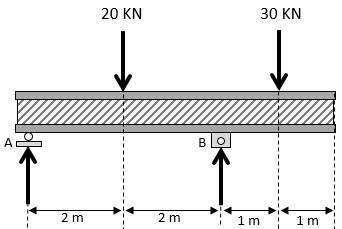
A opção que corresponde aos valores das reações RAy , RBy e RBx respectivamente, está na opção:
47,5 KN ; 2,5 KN e 0 KN
12KN ; 38 KN e 0 KN
12,5 KN ; 37,5 KN e 0 KN
2,5 KN ; 47,5 KN e 0 KN
12,5 KN ; 17,5 KN e 20 KN
Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra.
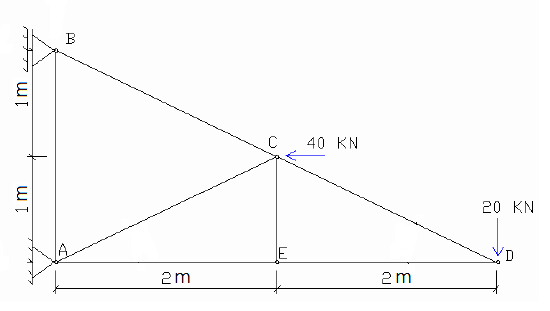
Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Determine o momento de inércia da área da seção transversal em relação ao eixo Y.
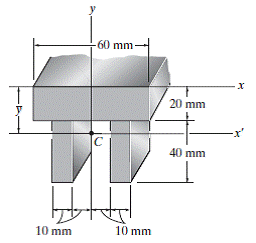
Iy = 18,9 .104 mm4
Iy = 45,2 .104 mm4
Iy = 42,5 .104 mm4
Iy = 34,8 .104 mm4
Iy = 54,7 .104 mm4
Determine o momento de inércia da peça da figura abaixo em relação ao eixo y.

Iy = 38.104 mm4
Iy = 23.104 mm4
Iy = 83.104 mm4
Iy = 74.104 mm4
Iy = 58.104 mm4
Determine a intensidade da força componente F na figura abaixo e a intensidade da força resultante se Fr estiver direcionada ao longo do eixo y positivo.
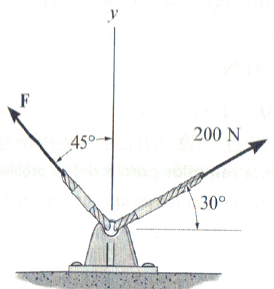
F = 271 N; Fr = 271 N
F = 129 N; Fr = 309 N
F = 225 N; Fr = 123 N
F = 245 N; Fr = 273 N
F = 157 N; Fr = 298 N
A viga de concreto da figura abaixo sustenta a estrutura de um galpão industrial, considerando as medidas descritas na figura, determine o centróide da área da seção transversal da viga de concreto.


1,2 m.
1,5 m.
2,5 m.
2 m.
1 m.
Determine o esforço cortante em C e o momento fletor em D da viga. Assuma que B seja um rolete e que C está localizado logo à direita da carga de 40 kN.

VC = 4,8 kN
MD = - 75,8 kN.m
VC = -3,33 kN
MD = 66,67 kN.m
VC = 2,5 kN
MD = 49,2 kN.m
VC = -2,45 kN
MD = 25,7 kN.m
VC = -6,66 kN
MD = 32,67 kN.m
O cubo da roda pode ser conectado ao eixo com deslocamento negativo (esquerda) ou com deslocamento positivo (direita). Se o pneu está sujeito às cargas normal e radial conforme mostrado,

Então o momento resultante dessas cargas em relação ao ponto O no eixo para os dois casos são respectivamente
200 N.m, 700 N.m
200 N.m, 800 N.m
120 N.m, 225 N.m
344 N.m, 225 N.m
350 N.m, 600 N.m
É correto afirmar em relação as intensidades das forças F1, F2 e F3, de modo que a partícula seja mantida em equilíbrio, que:

F2=F1
F1
F2
F1
F2
Calcule as reações de apoio,RAy , RBy e RBx do esquema abaixo (móvel em A, fixo em B):

A opção que corresponde aos valores das reações RAy , RBy e RBx respectivamente, está na opção:
47,5 KN ; 2,5 KN e 0 KN
12KN ; 38 KN e 0 KN
12,5 KN ; 37,5 KN e 0 KN
2,5 KN ; 47,5 KN e 0 KN
12,5 KN ; 17,5 KN e 20 KN
Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra.

Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Determine o momento de inércia da área da seção transversal em relação ao eixo Y.

Iy = 18,9 .104 mm4
Iy = 45,2 .104 mm4
Iy = 42,5 .104 mm4
Iy = 34,8 .104 mm4
Iy = 54,7 .104 mm4
Determine o momento de inércia da peça da figura abaixo em relação ao eixo y.

Iy = 38.104 mm4
Iy = 23.104 mm4
Iy = 83.104 mm4
Iy = 74.104 mm4
Iy = 58.104 mm4
Determine a intensidade da força componente F na figura abaixo e a intensidade da força resultante se Fr estiver direcionada ao longo do eixo y positivo.

F = 271 N; Fr = 271 N
F = 129 N; Fr = 309 N
F = 225 N; Fr = 123 N
F = 245 N; Fr = 273 N
F = 157 N; Fr = 298 N
A viga de concreto da figura abaixo sustenta a estrutura de um galpão industrial, considerando as medidas descritas na figura, determine o centróide da área da seção transversal da viga de concreto.


VC = 4,8 kN
MD = - 75,8 kN.m
VC = -3,33 kN
MD = 66,67 kN.m
VC = 2,5 kN
MD = 49,2 kN.m
VC = -2,45 kN
MD = 25,7 kN.m
VC = -6,66 kN
MD = 32,67 kN.m
O cubo da roda pode ser conectado ao eixo com deslocamento negativo (esquerda) ou com deslocamento positivo (direita). Se o pneu está sujeito às cargas normal e radial conforme mostrado,

Então o momento resultante dessas cargas em relação ao ponto O no eixo para os dois casos são respectivamente
200 N.m, 700 N.m
200 N.m, 800 N.m
120 N.m, 225 N.m
344 N.m, 225 N.m
350 N.m, 600 N.m
É correto afirmar em relação as intensidades das forças F1, F2 e F3, de modo que a partícula seja mantida em equilíbrio, que:

F2=F1
F1
F2
F1
F2
Calcule as reações de apoio,RAy , RBy e RBx do esquema abaixo (móvel em A, fixo em B):

A opção que corresponde aos valores das reações RAy , RBy e RBx respectivamente, está na opção:
47,5 KN ; 2,5 KN e 0 KN
12KN ; 38 KN e 0 KN
12,5 KN ; 37,5 KN e 0 KN
2,5 KN ; 47,5 KN e 0 KN
12,5 KN ; 17,5 KN e 20 KN
Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra.

Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Determine o momento de inércia da área da seção transversal em relação ao eixo Y.

Iy = 18,9 .104 mm4
Iy = 45,2 .104 mm4
Iy = 42,5 .104 mm4
Iy = 34,8 .104 mm4
Iy = 54,7 .104 mm4
Determine o momento de inércia da peça da figura abaixo em relação ao eixo y.

Iy = 38.104 mm4
Iy = 23.104 mm4
Iy = 83.104 mm4
Iy = 74.104 mm4
Iy = 58.104 mm4
Determine a intensidade da força componente F na figura abaixo e a intensidade da força resultante se Fr estiver direcionada ao longo do eixo y positivo.

F = 271 N; Fr = 271 N
F = 129 N; Fr = 309 N
F = 225 N; Fr = 123 N
F = 245 N; Fr = 273 N
F = 157 N; Fr = 298 N
A viga de concreto da figura abaixo sustenta a estrutura de um galpão industrial, considerando as medidas descritas na figura, determine o centróide da área da seção transversal da viga de concreto.


200 N.m, 700 N.m
200 N.m, 800 N.m
120 N.m, 225 N.m
344 N.m, 225 N.m
350 N.m, 600 N.m
É correto afirmar em relação as intensidades das forças F1, F2 e F3, de modo que a partícula seja mantida em equilíbrio, que:

F2=F1
F1
F2
F1
F2
Calcule as reações de apoio,RAy , RBy e RBx do esquema abaixo (móvel em A, fixo em B):

A opção que corresponde aos valores das reações RAy , RBy e RBx respectivamente, está na opção:
47,5 KN ; 2,5 KN e 0 KN
12KN ; 38 KN e 0 KN
12,5 KN ; 37,5 KN e 0 KN
2,5 KN ; 47,5 KN e 0 KN
12,5 KN ; 17,5 KN e 20 KN
Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra.

Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Determine o momento de inércia da área da seção transversal em relação ao eixo Y.

Iy = 18,9 .104 mm4
Iy = 45,2 .104 mm4
Iy = 42,5 .104 mm4
Iy = 34,8 .104 mm4
Iy = 54,7 .104 mm4
Determine o momento de inércia da peça da figura abaixo em relação ao eixo y.

Iy = 38.104 mm4
Iy = 23.104 mm4
Iy = 83.104 mm4
Iy = 74.104 mm4
Iy = 58.104 mm4
Determine a intensidade da força componente F na figura abaixo e a intensidade da força resultante se Fr estiver direcionada ao longo do eixo y positivo.

F = 271 N; Fr = 271 N
F = 129 N; Fr = 309 N
F = 225 N; Fr = 123 N
F = 245 N; Fr = 273 N
F = 157 N; Fr = 298 N
A viga de concreto da figura abaixo sustenta a estrutura de um galpão industrial, considerando as medidas descritas na figura, determine o centróide da área da seção transversal da viga de concreto.


F2=F1 F1 F2 F1 F2 Calcule as reações de apoio,RAy , RBy e RBx do esquema abaixo (móvel em A, fixo em B): A opção que corresponde aos valores das reações RAy , RBy e RBx respectivamente, está na opção: 47,5 KN ; 2,5 KN e 0 KN 12KN ; 38 KN e 0 KN 12,5 KN ; 37,5 KN e 0 KN 2,5 KN ; 47,5 KN e 0 KN 12,5 KN ; 17,5 KN e 20 KN Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra. Tracionando; Comprimindo; Tracionando; Tracionando. Comprimindo; Tracionando; Tracionando; Comprimindo. Tracionando; Comprimindo; Tracionando; Comprimindo. Tracionando; Comprimindo; Comprimindo; Comprimindo. Comprimindo; Comprimindo; Tracionando; Comprimindo. Determine o momento de inércia da área da seção transversal em relação ao eixo Y. Iy = 18,9 .104 mm4 Iy = 45,2 .104 mm4 Iy = 42,5 .104 mm4 Iy = 34,8 .104 mm4 Iy = 54,7 .104 mm4 Determine o momento de inércia da peça da figura abaixo em relação ao eixo y. Iy = 38.104 mm4 Iy = 23.104 mm4 Iy = 83.104 mm4 Iy = 74.104 mm4 Iy = 58.104 mm4 F = 271 N; Fr = 271 N F = 129 N; Fr = 309 N F = 225 N; Fr = 123 N F = 245 N; Fr = 273 N F = 157 N; Fr = 298 N A viga de concreto da figura abaixo sustenta a estrutura de um galpão industrial, considerando as medidas descritas na figura, determine o centróide da área da seção transversal da viga de concreto. 


Determine a intensidade da força componente F na figura abaixo e a intensidade da força resultante se Fr estiver direcionada ao longo do eixo y positivo.
